Indholdsfortegnelse:

Video: Hvordan laver du grundlæggende algebra?
2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
Til lave algebra , løs altid problemer ved hjælp af rækkefølgen af operationer, som er parenteser, eksponenter, multiplikation, division, addition og subtraktion. For eksempel vil du først løse det, der står i parentes, derefter løse eksponenterne og derefter gør enhver multiplikation og så videre.
Ved også, hvad er de grundlæggende regler for algebra?
Det Grundlæggende Love af Algebra er de associative, kommutative og distributive love. De hjælper med at forklare forholdet mellem taloperationer og giver mulighed for at forenkle ligninger eller løse dem. Arrangementet af tillæg påvirker ikke summen. Arrangementet af faktorer påvirker ikke produktet.
Ved siden af ovenstående, hvordan passerer du præ algebra? Fokuser på at lære det grundlæggende godt, og du vil være i stand til at bestå en udfordrende præ-algebratime med lethed.
- Præ-algebra terminologi. At huske ordforrådsord virker måske ikke som særlig sjovt, men præ-algebra er bygget på grundlæggende terminologi.
- Forstå ligninger.
- Spor dit arbejde.
- Få hjælp.
Ligeledes spørger folk, hvad bruger du algebra til?
Det mener nogle elever algebra er som at lære et andet sprog. Dette er i ringe grad sandt, algebra er et simpelt sprog, der bruges til at løse problemer, der ikke kan løses med tal alene. Den modellerer situationer i den virkelige verden ved at bruge symboler, såsom bogstaverne x, y og z til at repræsentere tal.
Hvad er formlerne for algebra?
Algebra formler
- (a + b) 2 = a 2 + b 2 + 2ab.
- (a − b) 2 = a 2 + b 2 − 2ab.
- -en 2 − b 2 = (a − b) (a + b)
- (x + a) (x + b) = x 2 + (a + b) x + ab.
- (a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca.
- (a + (-b) + (-c)) 2 = a 2 + (-b) 2 + (-c) 2 + 2a (−b) + 2 (−b) (−c) + 2a (−c) (a – b – c) 2 = a 2 + b 2 + c 2 − 2ab + 2bc − 2ca.
Anbefalede:
Hvordan bruger du det grundlæggende tælleprincip?

Det grundlæggende tælleprincip (også kaldet tællereglen) er en måde at finde ud af antallet af udfald i et sandsynlighedsproblem. Dybest set gange du begivenhederne sammen for at få det samlede antal udfald
Hvad er de grundlæggende udtryk i algebra?

Grundlæggende algebra-vilkår. Grundlæggende algebraudtryk, du skal kende, er konstanter, variable, koefficienter, led, udtryk, ligninger og andengradsligninger. Dette er nogle algebra-ordforråd, der vil være nyttige
Hvordan virker de fire grundlæggende kræfter?

Kræfter og bærerpartikler Der er fire grundlæggende kræfter, der virker i universet: den stærke kraft, den svage kraft, den elektromagnetiske kraft og gravitationskraften. De arbejder over forskellige områder og har forskellige styrker. Tyngdekraften er den svageste, men den har en uendelig rækkevidde
Hvordan gør cellestrukturer det muligt for en celle at udføre grundlæggende livsprocesser?
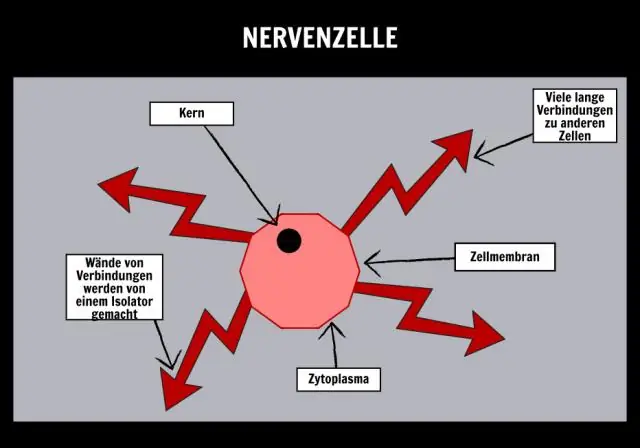
Specialiserede celler udfører særlige funktioner, såsom fotosyntese og energiomdannelse. op af cytoplasma, der er omgivet af en cellemembran og udfører de grundlæggende livsprocesser. og organel i en celle udfører visse processer, såsom fremstilling eller lagring af stoffer, der hjælper cellen med at holde sig i live
Hvordan hænger et trædiagram sammen med det grundlæggende tælleprincip?

Et trædiagram er en visuel visning af alle mulige udfald i en sammensat hændelse. Det grundlæggende tælleprincip siger, at hvis en begivenhed har m mulige udfald, og en anden uafhængig begivenhed har n mulige udfald, så er der m n mulige udfald for de to begivenheder tilsammen
