
Video: Hvordan løser man identitetsejendomme?

2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
Det Identitetsejendomme består af to dele: Additiv Identitet og multiplikativ Identitet . Tilføj nul (0) til et tal, summen er det tal. Gang et tal med 1, produktet er det tal. Divider et tal i sig selv, kvotienten er 1.
Spørgsmålet er også, hvad er et eksempel på identitetsejendomme?
Om Afskrift. Det identitetsejendomme af 1 siger, at ethvert tal ganget med 1 beholder sit identitet . Med andre ord forbliver ethvert tal ganget med 1 det samme. Grunden til, at tallet forbliver det samme, er, at gange med 1 betyder, at vi har 1 kopi af tallet. Til eksempel , 32x1=32.
Udover ovenstående, hvordan påvirker identitetsegenskaben tallene? Det identitetsejendomme af addition angiver, at summen af a nummer og nul er nummer . Hvis a er en rigtig nummer , derefter a+0=a. Det omvendte ejendom af tilføjelse angiver, at summen af enhver reel nummer og dens additive inverse (modsat) er nul. Hvis a er en rigtig nummer , derefter a+(-a)=0.
På samme måde spørges der, hvad er identitetsegenskaben?
Identitetsejendom . Det identitetsejendomme for addition fortæller os, at nul tilføjet til ethvert tal er selve tallet. Nul kaldes "tilsætningsstoffet identitet ." Det identitetsejendomme for multiplikation fortæller os, at tallet 1 ganget med et hvilket som helst tal giver selve tallet.
Hvad er identitetsegenskaben for 1?
Ifølge multiplikativet identitetsbesiddelse af 1 , ethvert tal ganget med 1 , giver samme resultat som selve tallet. Det kaldes også Identitetsejendom af multiplikation, fordi identitet af antallet forbliver det samme. Her er nogle eksempler på identitetsejendomme af multiplikation.
Anbefalede:
Hvordan løser man en andengradsligning ved hjælp af nulfaktorloven?

Af dette kan vi udlede, at: Hvis produktet af to vilkårlige tal er nul, så er det ene eller begge tal nul. Det vil sige, hvis ab = 0, så er a = 0 eller b = 0 (hvilket inkluderer muligheden for, at a = b = 0). Dette kaldes nulfaktorloven; og vi bruger det ofte til at løse andengradsligninger
Hvordan løser man ideel gaslov?

Ideal Gas Lov Formel Spørgsmål til Ideal Gas Lov Formel: Svar: Volumenet er V = 890,0mL og temperaturen er T = 21°C og trykket er P = 750mmHg. PV = nRT. Svar: Antallet af mol er n = 3,00 mol, temperaturen er T = 24°C og trykket er P = 762,4 mmHg. PV = nRT
Hvordan løser man totrinsligninger i præalgebra?

VIDEO På samme måde, hvad er de 4 trin til at løse en ligning? En 4-trins guide til løsning af ligninger (del 2) Trin 1: Forenkle hver side af ligningen. Som vi lærte sidst, er det første skridt i løsningen af en ligning at gøre ligningen så enkel som muligt.
Hvordan løser man gange og dividere brøker?
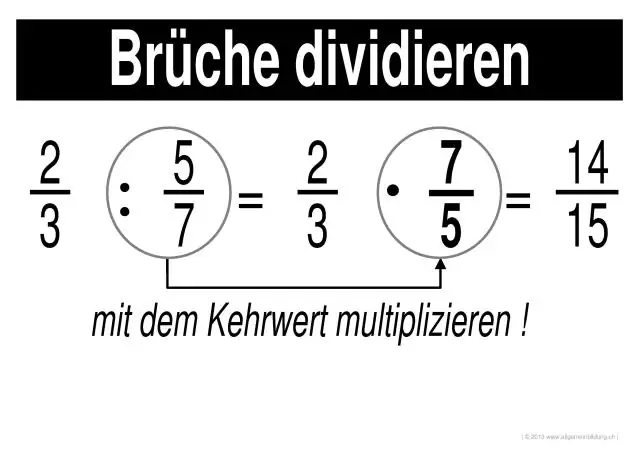
Gang og dividere brøker Trin 1: Gang tællere fra hver brøk med hinanden (tallene øverst). Resultatet er tælleren for svaret. Trin 2: Gang nævnerne for hver brøk med hinanden (tallene i bunden). Resultatet er nævneren for svaret. Trin 3: Forenkle eller reducere svaret
Hvordan løser man en eksponentregel?
Flyt kun de negative eksponenter. Produktregel: am ∙ an = am + n, dette siger, at for at gange to eksponenter med samme grundtal, beholder du grundtallet og adderer potenserne. Dette siger, at for at dividere to eksponenter med samme grundtal, beholder du grundtallet og trække magterne fra
