Hvorfor virker restsætningen?

Video: Hvorfor virker restsætningen?

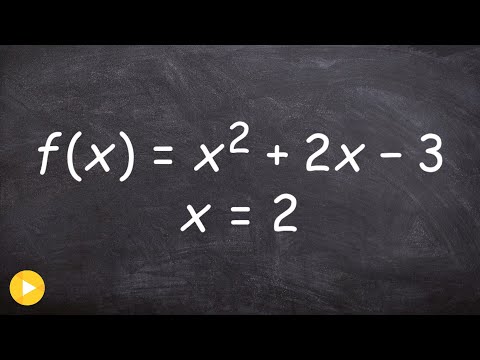
2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34

Det restsætning angiver, at f(a) er resten når polynomiet f(x) er divideret med x - a. Givet et polynomium, f(x), for at se, om et lineært binomium af formen x - a er et faktor af polynomiet løser vi for f(a). Hvis f(a) = 0, så er x - a a faktor , og x - a er ikke a faktor Ellers.

På samme måde bliver det spurgt, hvordan fungerer restsætningen?

Det restsætning siger følgende: Hvis du dividerer et polynomium f(x) med (x - h), så er den resten er f(h). Det teorem anfører, at vores resten er lig med f(h). Derfor har vi gør behøver ikke at bruge lang division, men skal blot evaluere polynomiet når x = h for at finde resten.

Man kan også spørge, hvad betyder en rest af 0? Hvis x - c er en faktor, kan du omskrive det oprindelige polynomium som (x - c) (kvotient). Du kan bruge syntetisk division til at hjælpe dig med denne type problemer. Det Resten Sætning siger, at f(c) = den resten . Så hvis resten kommer ud at være 0 når du anvender syntetisk division, så er x - c en faktor af f(x).

Ydermere, hvad er pointen med Remainder Theorem?

Det Restens sætning siger, at vi kan omformulere polynomiet i form af divisor, og derefter vurdere polynomiet ved x = a. Men når x = a, er faktoren "x – a" bare nul!

Er nul en rest?

Når et led ("udbyttet") divideres med et andet led ("divisor"), er resultatet en "kvotient" og en " resten ". Når resten er nul , er både kvotienten og divisoren faktorer for udbyttet. 0 er resten . Siden resten er nul , både 2 og 3 er faktorer på 6.

Anbefalede:

Hvorfor virker Oobleck som et fast stof og flydende?

Oobleck er en ikke-newtonsk væske, en betegnelse for væsker, der ændrer viskositet (hvor let de flyder) under stress. Denne frastødende kraft hjælper gyllen til at flyde, da partiklerne foretrækker et lag af væske mellem da. Men når de presses sammen, tager friktionen over, og partiklerne bevæger sig som et fast stof

Hvorfor virker princippet om lateral kontinuitet?

Princippet om lateral kontinuitet siger, at lag af sediment til at begynde med strækker sig lateralt i alle retninger; med andre ord, de er sideværts kontinuerlige. Som et resultat kan klipper, der ellers ligner hinanden, men som nu er adskilt af en dal eller andet erosionstræk, antages at være oprindeligt sammenhængende

Hvorfor virker Archimedes-princippet?

Hvis flydekraften er større end objektets vægt, vil objektet stige til overfladen og flyde. Arkimedes' princip siger, at den flydende kraft på en genstand er lig med vægten af den væske, den fortrænger. Vægtfylde er forholdet mellem densiteten af et objekt og en væske (normalt vand)

Hvorfor virker sporen grøn, mens cellekroppen fremstår lyserød?

Hvorfor virker sporen grøn, mens cellelegemet fremstår lyserødt i den færdige Endospore-farvning? Sporen virker grøn, fordi varmen tvang sporen til at optage det farvede farvestof, som let skylles ud, hvis cellekroppen