Hvordan laver du Fermats lille sætning?

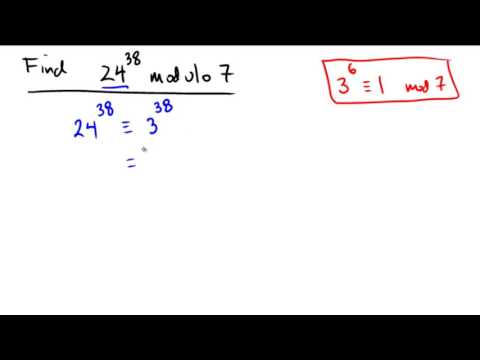
2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34

Fermats lille teorem angiver, at hvis p er et primtal, så for ethvert heltal a, tallet a ^s – a er et heltal af p. -en^s ≡ a (mod p). Særligt tilfælde: Hvis a ikke er deleligt med p, Fermats lille teorem svarer til udsagnet om, at a ^s-1-1 er et heltal af p.

Hvordan beviser man på denne måde Fermats lille sætning?

Lad p være et primtal og et hvilket som helst heltal, så a^s = a (mod p). Bevis. Resultatet er trival (begge sider er nul), hvis p deler a. Hvis p ikke deler a, skal vi kun gange kongruensen med Fermats lille sætning af a for at fuldføre beviset.

Ved også, hvad er løsningen på Fermats sidste sætning? Løsning til Fermats sidste sætning . Fermats sidste sætning (FLT), (1637), siger, at hvis n er et heltal større end 2, så er det umuligt at finde tre naturlige tal x, y og z, hvor en sådan lighed er opfyldt ved at være (x, y)>0 i xn+yn =zn.

I betragtning af dette, hvorfor er Fermats lille teorem vigtig?

Fermats lille teorem er en grundlæggende teorem i elementær talteori, som hjælper med at beregne potenser af heltal modulo primtal. Det er et særligt tilfælde af Eulers teorem , og er vigtig i anvendelser af elementær talteori, herunder primalitetstest og public-key kryptografi.

Hvad menes med Eulers sætning?

Eulers sætning . Generaliseringen af Fermats teorem er kendt som Eulers sætning . Generelt, Eulers sætning angiver, at "hvis p og q er relativt primtal, så", hvor φ er Eulers totient funktion for heltal. Det vil sige, er antallet af ikke-negative tal, der er mindre end q og relativt primtal til q.