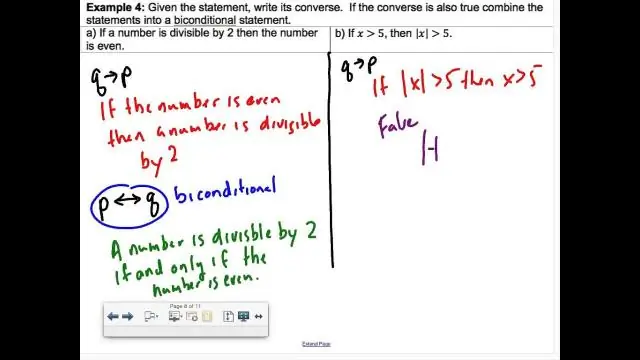
Video: Hvordan skriver man en Biconditional som to conditionals?

2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
Det er en kombination af to betingede udsagn, "hvis to linjestykker er kongruente, så er de lige lange" og "hvis to linjestykker er lige lange, så er de kongruente”. EN bibetinget er sandt, hvis og kun hvis begge betingelser er sande. Bi- betingelser repræsenteres af symbolet ↔ eller ⇔.
Ydermere, hvornår kan du skrive en bibetinget erklæring?
Hvornår du kombinere en betinget udmelding og det modsatte, du lave en betinget erklæring . EN betinget erklæring er en udmelding at kan skrives på formen "p hvis og kun hvis q." Dette betyder "hvis p, så q" og "hvis q, så p." Det bibetinget "p hvis og kun hvis q" kan også skrives som "p iff q" eller p ? q.
Ydermere, er kun hvis en Biconditional? HVIS OG KUN HVIS , er en bibetinget udsagn, hvilket betyder, at enten begge udsagn er sande eller begge er falske. Så det er i det væsentlige og HVIS ” udsagn, der virker begge veje.
Også at vide, hvad er betingede og bibetingede udsagn?
Når vi kombinerer to betingede erklæringer på denne måde har vi en bibetinget . Definition: A betinget erklæring defineres som sandt, når begge dele har samme sandhedsværdi. I sandhedstabellen ovenfor er p q sand, når p og q har de samme sandhedsværdier, (dvs. når begge er sande eller begge er falske).
Hvad er et eksempel på en bibetinget erklæring?
Eksempler på bibetingede erklæringer Det betingede udsagn for disse to sæt ville være: Polygonen har kun fire sider, hvis og kun hvis polygonen er en firkant. Polygonen er en firkant, hvis og kun hvis polygonen kun har fire sider.
Anbefalede:
Hvordan skriver man formlen for en forbindelse, der indeholder en polyatomisk ion?
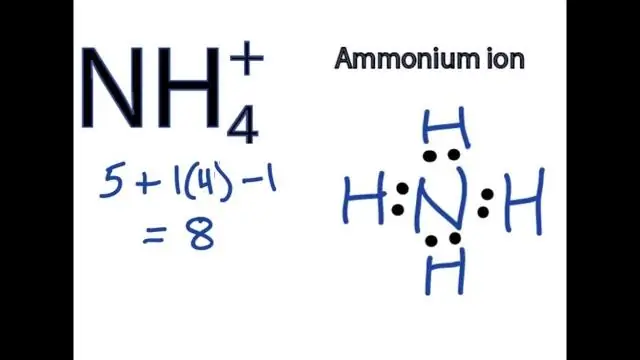
For at skrive formler for forbindelser, der indeholder polyatomiske ioner, skal du skrive symbolet for metalionen efterfulgt af formlen for den polyatomiske ion og afbalancere ladningerne. For at navngive en forbindelse, der indeholder en polyatomisk ion, angiv først kationen og derefter anionen
Hvordan skriver man 13/4 som et blandet tal?

Som en negativ uægte brøk (|tæller| > |nævner|): - 13/4 = - 13/4 Som et blandet tal. (et helt tal og en egen brøk, af samme tegn): - 13/4 = - 3 1/4 I procent: - 13/4 = - 325 %
Hvordan skriver man en brøk som et produkt af et helt tal og en enhedsbrøk?

Regler for at finde produktet af en enhedsbrøk og et helt tal Vi skriver først hele tallet som en brøk, dvs. skriver det divideret med en; for eksempel: 7 skrives som 71. Vi gange derefter tællerne. Vi multiplicerer nævnerne. Hvis der kræves nogen forenkling, er det gjort, og så skriver vi den sidste brøk
Hvordan skriver man som en brøk i enkleste form?
Når du skriver brøker i enkleste form, er der to regler at følge: Spørg om tælleren og nævneren kan divideres med det samme tal, som kaldes en fælles faktor. Se om mindst ét tal i brøken er et primenutal
Hvordan skriver man noget som funktion?

Du skriver funktioner med funktionsnavnet efterfulgt af den afhængige variabel, såsom f(x), g(x) eller endda h(t), hvis funktionen er afhængig af tid. Du læser funktionen f(x) som 'f af x' og h(t) som 'h af t'. Funktioner behøver ikke at være lineære
