Indholdsfortegnelse:

Video: Hvad er 3-delt definition af kontinuitet?
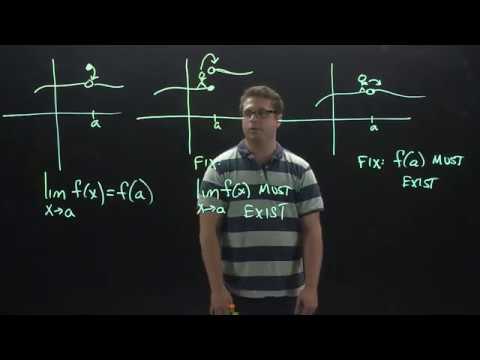
2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
En funktion f (x) er kontinuert i et punkt x = a, hvis følgende tre betingelser er opfyldt: Ligesom med det formelle definition af en grænse, den definition af kontinuitet præsenteres altid som en 3 - en del test, men tilstand 3 er den eneste, du skal bekymre dig om, fordi 1 og 2 er indbygget i 3.
Hvad er så den tredelte definition af kontinuitet?
En funktion f (x) er kontinuert i et punkt x = a, hvis følgende tre betingelser er opfyldt: Ligesom med det formelle definition af en grænse, den definition af kontinuitet præsenteres altid som en 3 - en del test, men tilstand 3 er den eneste, du skal bekymre dig om, fordi 1 og 2 er indbygget i 3.
Og hvad er grænsedefinitionen for kontinuitet? 1) Brug definition af kontinuitet baseret på grænser som beskrevet i videoen: Funktionen f(x) er kontinuerlig på det lukkede interval [a, b], hvis: a) f(x) eksisterer for alle værdier i (a, b), og. b) Tosidet begrænse af f(x) som x -> c er lig f(c) for enhver c i åbent interval (a, b), og.
I overensstemmelse hermed, hvad er de 3 betingelser for kontinuitet?
For at en funktion skal være kontinuert i et punkt fra en given side, har vi brug for følgende tre forhold : Funktionen er defineret ved punktet. funktionen har en grænse fra den side på det tidspunkt. den ensidige grænse er lig med værdien af funktionen i punktet.
Hvad er typerne af kontinuitet?
Hurtigt overblik
- Jump-diskontinuiteter: begge ensidige grænser findes, men har forskellige værdier.
- Uendelige diskontinuiteter: begge ensidige grænser er uendelige.
- Slutpunktsdiskontinuiteter: Kun én af de ensidige grænser eksisterer.
- Blandet: mindst en af de ensidige grænser eksisterer ikke.
Anbefalede:
Hvordan kontrollerer du kontinuitet på en CPC?

Test mellem linje og CPC ved hver udgang i kredsløbet. En læsning indikerer kontinuitet. Registrer testresultatet opnået ved det fjerneste punkt i kredsløbet. Denne værdi er (R1+R2) for kredsløbet
Hvad er kontinuitet på et multimeter?

Oversigt over kontinuitetstest Kontinuitet er tilstedeværelsen af en komplet vej for strømflow. Et kredsløb er færdigt, når dets kontakt er lukket. Når der testes for kontinuitet, bipper et multimeter baseret på modstanden af den komponent, der testes. Denne modstand bestemmes af multimeterets rækkeviddeindstilling
Hvilken definition er Bronsted Lowrys definition af en base?

En Bronsted-Lowry-syre er en kemisk art, der donerer en eller flere brintioner i en reaktion. I modsætning hertil accepterer en Bronsted-Lowry-base hydrogenioner. Når den donerer sin proton, bliver syren dens konjugerede base. Et mere generelt blik på teorien er en syre som en protondonor og en base som en protonacceptor
Hvad er kontinuitet og diskontinuitet i psykologi?

Kontinuitet kontra diskontinuitet. Kontinuitetssynet siger, at forandring er gradvis. Psykologer med diskontinuitetssynet mener, at mennesker gennemgår de samme stadier, i samme rækkefølge, men ikke nødvendigvis i samme hastighed; Hvis en person går glip af et stadie, kan det dog have varige konsekvenser
Hvad er en kontinuitet i calculus?

Hvad er kontinuitet? I calculus er en funktion kontinuert ved x = a, hvis - og kun hvis - alle tre af følgende betingelser er opfyldt: Funktionen er defineret ved x = a; dvs. f(a) er lig med et reelt tal. Grænsen for funktionen, når x nærmer sig a, eksisterer
