Indholdsfortegnelse:

Video: Hvordan kan man se, om funktionen konvergerer eller divergerer?

2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
Hvis du har en serie det er mindre end en konvergent benchmark serier, så skal din serie også konvergere . Hvis benchmark konvergerer , din serie konvergerer ; og hvis benchmark divergerer , din serie divergerer . Og hvis din serie er større end en divergerende benchmark-serie, så skal din serie også afvige.
Desuden, hvordan ved du, om en grænse konvergerer eller divergerer?
Du kan opsummere det hele i en sætning: Hvis graden af tælleren er den samme som graden af nævneren, så sekvens konvergerer til forholdet mellem de førende koefficienter (4/3 i eksemplet); hvis nævneren har en højere grad, så den sekvens konvergerer til 0; hvis tælleren har en højere grad, Ved siden af ovenstående, hvorfor konvergerer og divergerer 1 n/2? Ved at fortsætte i på denne måde kan du se serien Σ1/ som summen af uendeligt mange "grupperinger", alle med værdi større end 1 / 2 . Altså serien divergerer , for hvis man lægger op 1 / 2 nok gange, vil summen i sidste ende blive så stor, som du vil. Lad os prøve at finde denne sum ved hjælp af en anden serie.
Simpelthen så, konvergerer eller divergerer 1/2 n?
Summen af 1/2 ^ n konvergerer , så 3 gange er det også konvergerer . Siden summen af 3 divergerer , og summen af 1/2 ^ n konvergerer , serien divergerer . Du skal dog være forsigtig her: hvis du får en sum på to divergerende serier, af og til vil de annullere hinanden, og resultatet vil konvergere.
Hvordan kan man se, om en sekvens er afgrænset?
Hvis sekvensen både er afgrænset under og afgrænset over, kalder vi sekvensen afgrænset
- Bemærk, at for at en sekvens skal være stigende eller faldende, skal den være stigende/faldende for hver n.
- En sekvens er afgrænset nedenfor, hvis vi kan finde et hvilket som helst tal m, således at m≤an m ≤ a n for hver n.
Anbefalede:
Hvad sker der, når plader støder sammen og divergerer?

Divergent (spredning): Det er her to plader bevæger sig væk fra hinanden. Konvergent (kolliderer): Dette sker, når plader bevæger sig mod hinanden og kolliderer. Når en kontinentalplade møder en oceanisk plade, synker den tyndere, tættere og mere fleksible oceaniske plade ned under den tykkere, mere stive kontinentalplade
Hvordan kan man se, om en polynomisk graf er positiv eller negativ?
Hvis graden er ulige, og den førende koefficient er positiv, peger venstre side af grafen nedad, og højre side peger op. Hvis graden er ulige og den førende koefficient er negativ, peger venstre side af grafen op og højre side ned
Hvordan finder man funktionen af en cirkel?
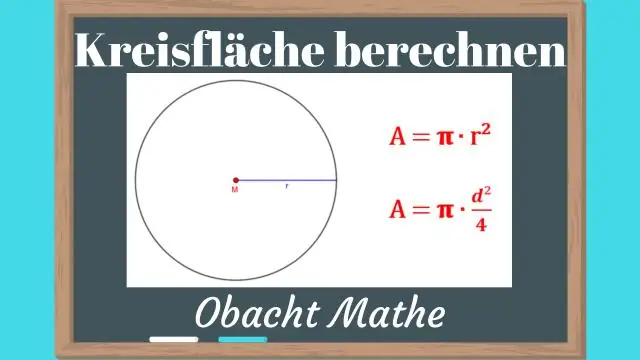
Cirkelligningens centrum-radiusform er i formatet (x – h)2 + (y – k)2= r2, hvor centrum er i punktet (h, k) og radius er 'r'. Denne form for ligningen er nyttig, da du nemt kan finde centrum og radius
Hvad dannes i de områder, hvor oceaniske plader divergerer og ny havbund skabes afgrundshøjde sletter, kontinentalsokkel, kontinentalskråning midt på havets højderyg?

Kontinentalskråningen og stigningen er overgangsbestemt mellem skorpetyper, og afgrundssletten er underlagt mafisk oceanisk skorpe. Oceaniske højderygge er divergerende pladegrænser, hvor ny oceanisk lithosfære dannes, og oceaniske skyttegrave er konvergerende pladegrænser, hvor oceanisk litosfære er subduceret
Hvordan ved man, om en potensrække konvergerer?

Resultater på geometriske serier viser, at de to udtryk er ens. De to udtryk er ikke ens; faktisk afviger serien til højre ved Zero Limit Test. Du kan bruge forholdstesten (og nogle gange rodtesten) til at bestemme de værdier, som en potensrække konvergerer for
