
Video: Hvordan skriver man domænet for en ulighed?

2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
Som en ulighed , vi ville skrive Læs som "den domæne af funktionen er alle værdier af x, der er større end eller lig med nul". For mere om uligheder se Uligheder . I såkaldt intervalnotation har den samme funktion en domæne af Dette beskriver værdisættet fra 0 til positiv uendelig.
Desuden, hvordan finder man domænet for en ulighed?
Til finde domænet , løse ulighed 4 - x > 0. x < 4. Således repræsenterer alle tal mindre end eller lig med 4 domæne til denne funktion. Når man prøver at finde domænet og spænder fra en graf, den domæne findes ved at se på grafen fra venstre mod højre.
Efterfølgende er spørgsmålet, hvad er domæne i funktionsnotation? Det domæne af en fungere er det komplette sæt af mulige værdier for den uafhængige variabel. På almindeligt engelsk betyder denne definition: The domæne er mængden af alle mulige x-værdier, som vil gøre fungere "arbejde", og vil udsende reelle y-værdier.
Ved også, hvordan skriver man et domæne i intervalnotation?
Det er generelt meget nemmere at se på en funktions ligning og finde ud af dens domæne end det er at finde ud af dens rækkevidde. Tag for eksempel f(x)=x+2x−3. Det kan vi se domæne er alle reelle tal undtagen 3. In intervalnotation der er skrevet (−∞, 3)∪(3, ∞).
Hvad er rækkevidden af ulighed?
Rækkevidde er mængden af alle y-værdier, den afhængige mængde, der vil resultere ved at substituere alle x-værdier (domænet) i funktionen. Så rækkevidde af f(x) = 2x + 3 er også alle reelle tal, for uanset hvilken værdi af x er, kan vi altid gange det tal med 2 og lægge 3 sammen.
Anbefalede:
Hvordan finder man skæringerne af en ulighed?
Alternativt kan vi bestemme x-skæringspunktet og y-skæringspunktet for standardformen lineær lighed ved at substituere y = 0, derefter løse for x og substituere x = 0, derefter løse for henholdsvis y. Husk, at x-skæringspunktet er værdien af x, når y = 0, og de-skæringspunktet er værdien af y, når x = 0
Hvordan skygger man området for en ulighed?
Der er tre trin: Omarranger ligningen, så 'y' er til venstre og alt andet til højre. Plot 'y='-linjen (gør den til en ubrudt linje for y≤ eller y≥ og en stiplet linje for y) Skygge over linjen for en 'større end' (y> eller y≥) eller under linjen for en 'mindre end' (y< eller y≤)
Hvordan afgør man, om en ulighed ikke har nogen løsning?

Isoler det absolutte værdiudtryk på venstre side af uligheden. Hvis tallet på den anden side af ulighedstegnet er negativt, har din ligning enten ingen løsning eller alle reelle tal som løsninger. Brug tegnet på hver side af din ulighed til at afgøre, hvilke af disse sager der gælder
Hvordan finder man domænet for en begrænsning i en ligning?

Sådan gør du: Givet en funktion skrevet i en ligningsform, der inkluderer en brøk, skal du finde domænet. Identificer inputværdierne. Identificer eventuelle begrænsninger for input. Hvis der er en nævner i funktionens formel, skal du sætte nævneren lig med nul og løse for x
Hvordan finder man domænet for en algebraisk funktion?
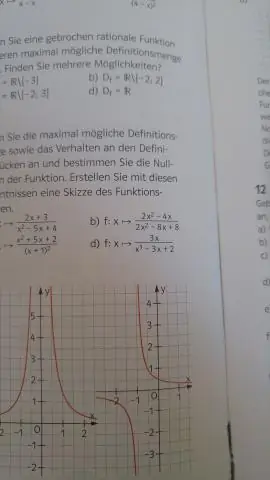
En funktions domæne er sættet af alle mulige input til funktionen. For eksempel er domænet for f(x)=x² alle reelle tal, og domænet for g(x)=1/x er alle reelle tal undtagen x=0
