
Video: Hvad er summen af geometriske rækker?
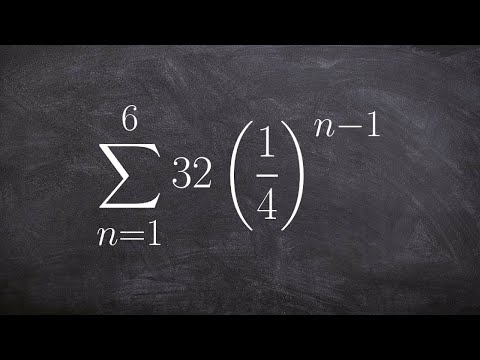
2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
For en uendelig geometriske serier at have en sum , skal det fælles forhold r være mellem −1 og 1. For at finde sum af en uendelig geometriske serier har forhold med en absolut værdi mindre end én, brug formlen S=a11−r, hvor a1 er det første led, og r er det fælles forhold.
Hvordan finder man derfor summen af en geometrisk række?
Til find summen af en endelig geometriske serier , brug formel , Sn=a1(1−rn)1−r, r≠1, hvor n er antallet af led, a1 er det første led, og r er det fælles forhold.
Derudover, hvad er formlen for geometrisk progression? I matematik, en geometrisk progression ( rækkefølge ) (også unøjagtigt kendt som en geometriske serier ) er en rækkefølge af tal, således at kvotienten af to på hinanden følgende medlemmer af rækkefølge er en konstant kaldet det fælles forhold mellem rækkefølge . Det geometrisk progression kan skrives som: ar0=a, ar1=ar, ar2, ar3, På samme måde kan man spørge, hvad er summen af uendelige geometriske rækker?
An uendelig geometrisk række er sum af en uendelig geometrisk rækkefølge . Det her serie ville ikke have nogen sidste periode. Den generelle form for uendelig geometrisk række er a1+a1r+a1r2+a1r3+, hvor a1 er det første led, og r er det fælles forhold. Vi kan finde sum af alle endelige geometriske serier.
Hvad er formlen for summen af geometrisk progression?
Geometrisk Progression Den generelle form for en praktiserende læge er a, ar, ar2, ar3 og så videre. Den n. semester af en praktiserende læge serie er T = ar -1, hvor a = første led og r = fælles forhold = T /T -1). Det sum af en praktiserende læges uendelige vilkår serie S∞= a/(1-r) hvor 0< r<1.
Anbefalede:
Hvad er formålet med geometriske konstruktioner?

'Konstruktion' i geometri betyder at tegne figurer, vinkler eller linjer nøjagtigt. Disse konstruktioner bruger kun kompas, straightedge (dvs. lineal) og en blyant. Dette er den 'rene' form for geometrisk konstruktion: ingen tal involveret
Hvad er den geometriske middelværdi af 4 og 18?

+15. Muxakara og 15 andre lærte af dette svar. √(4×18)= √72 eller √36√2= 6√2 forenklet
Hvad er den geometriske form af Allene?

Det centrale carbon er sp-hybridiseret, og de to terminale carbonatomer er sp2-hybridiseret. Bindingsvinklen dannet af de tre carbonatomer er 180°, hvilket indikerer lineær geometri for det centrale carbonatom. De to terminale carbonatomer er plane, og disse planer er snoet 90° fra hinanden
Hvad er de geometriske begreber?

Nogle grundlæggende geometrikoncepter, ord og notationer, som du skal vide, er punkter, linjer, linjestykker, midtpunkter, stråler, planer og rum
Hvorfor stiller økologer spørgsmål om begivenheder og organismer, der rækker?

Hvorfor stiller økologer spørgsmål om begivenheder og organismer, der varierer i kompleksitet fra et individ til biosfæren? For at forstå sammenhænge inden for biosfæren stiller økologer spørgsmål om begivenheder og organismer, der varierer i kompleksitet fra et enkelt individ til hele biosfæren
