
Video: Er en matrix magen til dens inverse?

2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
Tænk bare på en 2x2 matrix det er ligner dens omvendte uden at de diagonale indtastninger er 1 eller -1. Diagonal matricer vil gøre. Altså A og omvendt af A er lignende , så deres egenværdier er de samme. hvis en af A's egenværdier er n, er en egenværdi på dens omvendte vil være 1/n.
Også spurgt, ligner en matrix dens transponering?
Enhver firkant matrix over en mark er ligner dens omsætning og ethvert kvadratisk kompleks matrix er lignende til et symmetrisk kompleks matrix.
Ligeledes er alle inverterbare matricer ens? Hvis A og B er lignende og invertibel , så er A–1 og B–1 lignende . Bevis. Siden alle det matricer er invertibel , vi kan tage det omvendte af begge sider: B–1 = (P–1AP)–1 = P–1A–1(P–1)–1 = P–1A–1P, så A–1 og B–1 er lignende . Hvis A og B er lignende , så er Ak og Bk for enhver k = 1, 2,.
Med hensyn til dette, kan en matrix ligne sig selv?
Det vil sige enhver matrix er ligner sig selv : I−1AI=A. Hvis A er lignende til B, så er B lignende til A: hvis B=P−1AP, så A=PBP−1=(P−1)−1BP−1. Hvis A er lignende til B via B=P−1AP, og C er lignende til B via C=Q−1BQ, så er A lignende til C: C=Q−1P−1APQ=(PQ)−1APQ.
Hvad betyder det, hvis matricer er ens?
I lineær algebra, to n-for-n matricer A og B kaldes lignende hvis der eksisterer en invertibel n-for-n matrix P sådan at. Lignende matricer repræsentere det samme lineære kort under to (muligvis) forskellige baser, hvor P er ændringen af basis matrix.
Anbefalede:
Hvordan relaterer ordet matrix til mitokondrier?
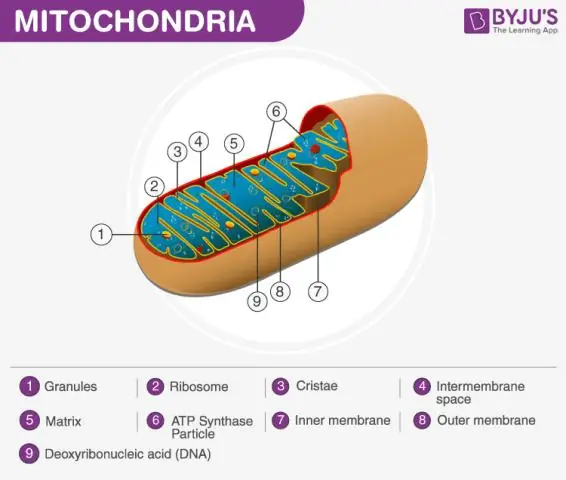
Mitokondriematricen defineret Mitokondriet består af en ydre membran, en indre membran og et gel-lignende materiale kaldet matrixen. Denne matrix er mere tyktflydende end cellens cytoplasma, da den indeholder mindre vand. Dette er et vigtigt trin i cellulær respiration, som producerer energimolekyler kaldet ATP
Hvordan er mængden af gasser relateret til dens temperatur og tryk?

Volumenet af en given mængde gas er omvendt proportional med dets tryk, når temperaturen holdes konstant (Boyles lov). Under de samme temperatur- og trykforhold indeholder lige store volumener af alle gasser det samme antal molekyler (Avogadros lov)
Hvordan gør man en matrix til en identitetsmatrix?

VIDEO Desuden, hvordan finder du det omvendte af en matrix ved hjælp af en identitetsmatrix? Det fungerer på samme måde for matricer . Hvis du gange a matrix (såsom A) og dens omvendt (i dette tilfælde A – 1 ), får du identitetsmatrix I.
HVORDAN ER en Stars farve relateret til dens temperatur?

Stjerner med overfladetemperaturer op til 3.500°C er røde. Skygge en lodret søjle fra 2.000°C til 3.500°C en lys rød. Skygge andre farvesøjler som følger: Stjerner op til 5.000°C er orange-røde; op til 6.000°C gul-hvid; op til 7.500°C blå-hvid og op til 40.000°C blå
Hvordan finder man den additive inverse af en matrix?

For at få additiv invers af given matrix, skal vi bare gange hvert element i matrix med -1. Når vi multiplicerer hvert element i matrix med -1, bliver det lig med -A. Derfor bliver A+(-A) lig med 0, hvor 0 er en nulmatrix. Det opfylder den grundlæggende definition af additiv invers
