
Video: Kan summen af en aritmetisk række være negativ?

2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
Opførselen af aritmetisk rækkefølge afhænger af den fælles forskel d. Hvis den fælles forskel, d, er: Positiv, den sekvens vil fremskridt mod det uendelige (+∞) Negativ , det sekvens vil regress mod negativ uendelig (−∞)
Desuden, kan summen af en serie være negativ?
Du taler om sum af en uendelig serie hvilket indebærer, at serie er geometrisk, da en uendelig aritmetik serie kan aldrig konvergere. Husk, det fælles forhold skal være |r| < 1 for en sum at eksistere. Altså hvis fællesforholdet er positivt der kan være nej negativ sum.
Og hvad er summen af endelige aritmetiske rækker? Det sum af (n) vilkår for en aritmetiske rækker er (5{n}^{2}-11n) for alle værdier af (n). Bestem den fælles forskel. Det sum af en aritmetiske rækker er (ext{100}) gange sin første term, mens den sidste term er (ext{9}) gange den første term.
Heraf, hvordan finder man summen af en aritmetisk række?
Til Find det sum af en aritmetik sekvens, start med at identificere det første og sidste nummer i sekvensen. Læg derefter disse tal sammen og divider sum med 2. Gang til sidst dette tal med det samlede antal led i rækkefølgen til Find det sum.
Hvad er N i serien?
Det første led er en1, den fælles forskel er d, og antallet af led er. Summen af en aritmetik serie findes ved at gange antallet af led gange gennemsnittet af første og sidste led. For at finde skal du bruge den eksplicitte formel for en aritmetik rækkefølge . Vi løser 3 + (– 1)·4 = 99 for at få = 25.
Anbefalede:
Kan chi kvadrat være negativ?
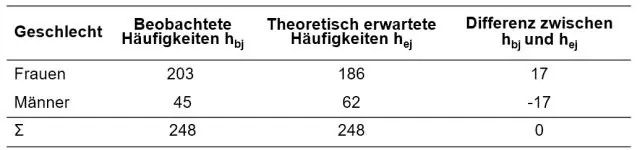
Mener du: Kan værdier af chi kvadrat nogensinde være negative? Svaret er nej. Værdien af et chi-kvadrat kan ikke være negativt, fordi det er baseret på summen af kvadratiske forskelle (mellem opnåede og forventede resultater)
Hvad er summen af den aritmetiske række?

Summen af en aritmetisk række findes ved at gange antallet af led gange gennemsnittet af første og sidste led. Eksempel: 3 + 7 + 11 + 15 + ··· + 99 har a1 = 3 og d = 4
Kan en negativ og positiv hældning være parallelle?

Sætning 104: Hvis to linjer har samme hældning, så er linjerne ikke-lodrette parallelle linjer. Hvis to linjer er vinkelrette, og ingen af dem er lodrette, så har en af linjerne en positiv hældning, og den anden har en negativ hældning. Også de absolutte værdier af deres skråninger er gensidige
Kan elastisk potentiel energi være negativ?

Fordi du arbejder på fjederen, dvs. overfører energi til den, øger du den potentielle energi, der er lagret i den. At lave den fornuftige definition, at PE er nul, når x=0, kan den potentielle energi aldrig være negativ
Hvordan finder man summen af en endelig aritmetisk eller geometrisk række?

Formlen for summen af n led i en geometrisk sekvens er givet ved Sn = a[(r^n - 1)/(r - 1)], hvor a er det første led, n er lednummeret og r er det første led. fælles forhold
