Indholdsfortegnelse:

Video: Hvordan løser man koefficienten ved at udfylde kvadratet?

2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
Nu kan vi løse en andengradsligning i 5 trin:
- Trin 1 Divider alle led med a (den koefficient af x2).
- Trin 2 Flyt talleddet (c/a) til højre side af ligningen.
- Trin 3 Fuldfør firkanten på venstre side af ligningen og afbalancer dette ved at tilføje den samme værdi til højre side af ligningen.
Hvad er koefficienter på denne måde?
I matematik, en koefficient er en multiplikationsfaktor i et eller andet led af et polynomium, en række eller et hvilket som helst udtryk; det er normalt et tal, men kan være et hvilket som helst udtryk. For eksempel, hvis y betragtes som en parameter i ovenstående udtryk, vil koefficient af x er −3y, og konstanten koefficient er 1,5 + år.
For det andet, hvornår kan du ikke fuldføre pladsen? Forresten, medmindre du bliver fortalt det du skal bruge færdiggørelse af pladsen , du vil Brug sandsynligvis aldrig denne metode i praksis, når du løser andengradsligninger. Enten en anden metode (såsom factoring) vilje være indlysende og hurtigere, ellers er den kvadratiske formel (gennemgået næste) vilje være nemmere at bruge.
Hvilken konstant skal derfor tilføjes for at fuldføre firkanten?
Det konstant hvilken skal tilføjes og subtraheret er (B) 1/64. bruges til at løse andengradsligningen med udfylde kvadratet.
Hvornår skal jeg færdiggøre firkanten?
Dernæst, hvis koefficienten for det kvadratiske led er 1 og koefficienten for det lineære (midterste) led er lige, færdiggørelse af pladsen er en god metode til brug. Til sidst vil andengradsformlen fungere på enhver andengradsligning.
Anbefalede:
Hvordan løser man en andengradsligning ved hjælp af nulfaktorloven?

Af dette kan vi udlede, at: Hvis produktet af to vilkårlige tal er nul, så er det ene eller begge tal nul. Det vil sige, hvis ab = 0, så er a = 0 eller b = 0 (hvilket inkluderer muligheden for, at a = b = 0). Dette kaldes nulfaktorloven; og vi bruger det ofte til at løse andengradsligninger
Hvordan løser man et system med tre ligninger ved eliminering?

Vælg et andet sæt af to ligninger, f.eks. ligning (2) og (3), og eliminer den samme variabel. Løs systemet skabt af ligning (4) og (5). Erstat nu z = 3 i ligning (4) for at finde y. Brug svarene fra trin 4 og indsæt i enhver ligning, der involverer den resterende variabel
Hvordan løser man et lineært programmeringsproblem ved hjælp af hjørnemetoden?
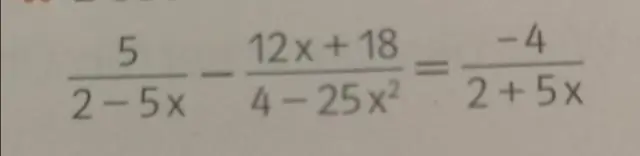
HJØRNEMETODEN Tegn grafen for det mulige sæt (region), S. Find de NØJAGTIGE koordinater for alle toppunkter (hjørnepunkter) af S. Evaluer objektivfunktionen, P, ved hvert hjørne Maksimum (hvis det findes) er den største værdi af P ved et toppunkt. Minimum er den mindste værdi af P ved et toppunkt
Hvordan løser man en ligning ved at isolere variablen?
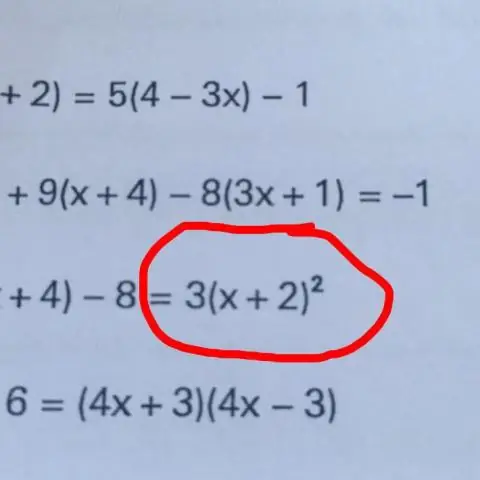
Den grundlæggende teknik til at isolere en variabel er at "gøre noget på begge sider" af ligningen, såsom at addere, subtrahere, gange eller dividere begge sider af ligningen med det samme tal. Ved at gentage denne proces kan vi få variablen isoleret på den ene side af ligningen
Hvordan løser man en lineær ligning ved hjælp af Gauss elimination?

Sådan bruges Gauss-eliminering til at løse ligningssystemer Du kan gange enhver række med en konstant (bortset fra nul). gange række tre med –2 for at give dig en ny række tre. Du kan skifte mellem to rækker. bytter række et og to. Du kan tilføje to rækker sammen. tilføjer række et og to og skriver det i række to
