Indholdsfortegnelse:

Video: Hvordan løser man en lineær ligning ved hjælp af Gauss elimination?

2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
Sådan bruges Gauss-eliminering til at løse ligningssystemer
- Du kan gange enhver række ved en konstant (andre end nul). gange række tre ved –2 for at give dig en ny række tre.
- Du kan skifte mellem to rækker. bytter række et og to.
- Du kan tilføje to rækker sammen. tilføjer række et og to og skriver det i række to.
Så hvordan virker Gaussisk eliminering?
Løst sagt, Gaussisk eliminering virker fra toppen og ned for at producere en matrix i echelonform, hvorimod Gauss - Jordan eliminering fortsætter hvor Gaussisk slap ved derefter at arbejde nedefra og op for at producere en matrix i reduceret echelon-form. Teknikken vil blive illustreret i det følgende eksempel.
Desuden, hvad er Cramers regelmatricer? Cramers regel til et 2×2-system (med to variable) Cramers regel er en anden metode, der kan løse systemer af lineære ligninger ved hjælp af determinanter. Med hensyn til notationer, en matrix er en matrix af tal omgivet af firkantede parenteser mens determinant er en matrix af tal omgivet af to lodrette streger.
For det andet, hvad er formålet med gaussisk eliminering?
Gaussisk eliminering . Fra Wikipedia, den frie encyklopædi. Gaussisk eliminering , også kendt som rækkereduktion, er en algoritme i lineær algebra til løsning af et system af lineære ligninger. Det forstås normalt som en sekvens af operationer udført på den tilsvarende matrix af koefficienter.
Hvad er forskellen mellem Gaussisk og Gauss Jordan-eliminering?
3 svar. Gaussisk Elimination hjælper med at sætte en matrix i række echelon form, mens Gauss - Jordan Elimination sætter en matrix i reduceret række echelon form. For små systemer (eller i hånden) er det normalt mere bekvemt at bruge Gauss - Jordan eliminering og løs eksplicit for hver repræsenteret variabel i matrix system.
Anbefalede:
Hvordan løser man en andengradsligning ved hjælp af nulfaktorloven?

Af dette kan vi udlede, at: Hvis produktet af to vilkårlige tal er nul, så er det ene eller begge tal nul. Det vil sige, hvis ab = 0, så er a = 0 eller b = 0 (hvilket inkluderer muligheden for, at a = b = 0). Dette kaldes nulfaktorloven; og vi bruger det ofte til at løse andengradsligninger
Hvordan løser man en lineær ulighedsligning?

Der er tre trin: Omarranger ligningen, så 'y' er til venstre og alt andet til højre. Plot 'y='-linjen (gør den til en ubrudt linje for y≤ eller y≥ og en stiplet linje for y) Skygge over linjen for en 'større end' (y> eller y≥) eller under linjen for en 'mindre end' (y< eller y≤)
Hvordan ved man, om en ligning er lineær eller ikke-lineær?

Brug af en ligning Simplificere ligningen så tæt som muligt på formen af y = mx + b. Tjek om din ligning har eksponenter. Hvis den har eksponenter, er den ikke-lineær. Hvis din ligning ikke har nogen eksponenter, er den lineær
Hvordan løser man et lineært programmeringsproblem ved hjælp af hjørnemetoden?
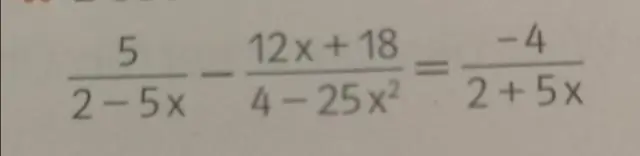
HJØRNEMETODEN Tegn grafen for det mulige sæt (region), S. Find de NØJAGTIGE koordinater for alle toppunkter (hjørnepunkter) af S. Evaluer objektivfunktionen, P, ved hvert hjørne Maksimum (hvis det findes) er den største værdi af P ved et toppunkt. Minimum er den mindste værdi af P ved et toppunkt
Hvordan løser man en ligning ved at isolere variablen?
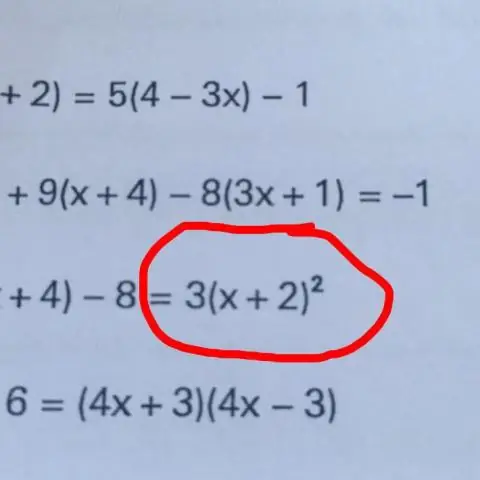
Den grundlæggende teknik til at isolere en variabel er at "gøre noget på begge sider" af ligningen, såsom at addere, subtrahere, gange eller dividere begge sider af ligningen med det samme tal. Ved at gentage denne proces kan vi få variablen isoleret på den ene side af ligningen
