
Video: Hvorfor har rationelle funktioner begrænsninger?

2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
Domæne restriktioner af en rationel funktion kan bestemmes ved at sætte nævneren lig med nul og løse. De x -værdier, hvor nævneren er lig med nul er kaldet singulariteter og er ikke i domænet af fungere.
Ligeledes, hvorfor er rationelle funktioner vigtige?
Betydning. " Rationel funktion " er navnet givet til en fungere som kan repræsenteres som kvotienten af polynomier, ligesom en rationel tal er et tal, der kan udtrykkes som en kvotient af hele tal. Rationelle funktioner levere vigtig eksempler og forekommer naturligt i mange sammenhænge.
Ligeledes har rationelle funktioner vendepunkter? 4 Sammenfatning. Et polynomium af grad n har højst n reelle nuller og n−1 vendepunkter . EN rationel funktion er en fungere af formen f(x)=P(x)Q(x), f (x) = P (x) Q (x), hvor P(x) og Q(x) er begge polynomier.
Spørgsmålet er også, hvad er et rationel funktionseksempel?
Eksempler af Rationelle funktioner Det fungere R(x) = (x^2 + 4x - 1) / (3x^2 - 9x + 2) er en rationel funktion da tælleren, x^2 + 4x - 1, er et polynomium og nævneren, er 3x^2 - 9x + 2 også et polynomium.
Hvad er kendetegnene ved rationelle funktioner?
To vigtige funktioner af enhver rationel funktion r(x)=p(x)q(x) r (x) = p (x) q (x) er alle nuller og lodrette asymptoter fungere kan have. Disse aspekter af en rationel funktion er tæt forbundet med, hvor henholdsvis tæller og nævner er nul.
Anbefalede:
Er heltal altid nogle gange eller aldrig rationelle tal?

1,5 er et rationelt tal, der kan skrives som: 3/2 hvor 3 og 2 begge er heltal. Her er det rationelle tal 8 et heltal, men det rationelle tal 1,5 er ikke et heltal, da 1,5 ikke er et helt tal. Så vi kan sige, at et rationelt tal er et heltal nogle gange ikke altid. Derfor er det rigtige svar nogle gange
Hvorfor angiver vi restriktioner for rationelle udtryk, og hvornår angiver vi restriktionerne?

Vi angiver begrænsninger, fordi det kan forårsage, at ligningen er udefineret i nogle værdier af x. Den mest almindelige begrænsning for rationelle udtryk er N/0. Det betyder, at ethvert tal divideret med nul er udefineret. For eksempel, for funktionen f(x) = 6/x², når du erstatter x=0, vil det resultere til 6/0, hvilket er udefineret
Hvordan anvender jeg dimensionelle begrænsninger i AutoCAD?
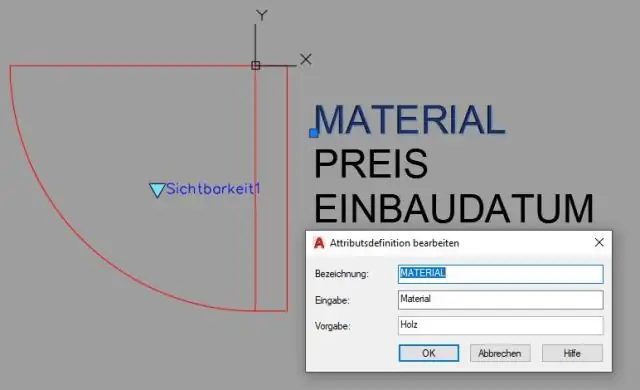
Disse trin præsenterer et simpelt eksempel på dimensionelle begrænsninger: Start en ny tegning og gør båndets Parametriske fane aktuel. Slå de relevante præcisionstegningshjælpemidler til på statuslinjen, såsom Snap, Ortho og Osnap. Tegn en nogenlunde præcis geometri ved at anvende en præcisionsteknik
Hvorfor kaldes trigonometriske funktioner cirkulære funktioner?

Trigonometriske funktioner kaldes nogle gange cirkulære funktioner. Dette skyldes, at de to grundlæggende trigonometriske funktioner - sinus og cosinus - er defineret som koordinaterne for et punkt P, der bevæger sig rundt på enhedscirklen med radius 1. Sinus og cosinus gentager deres udgange med regelmæssige intervaller
Hvordan multiplicerer man rationelle funktioner?

Q og S er ikke lig med 0. Trin 1: Faktorer både tælleren og nævneren. Trin 2: Skriv som en brøk. Trin 3: Forenkle det rationelle udtryk. Trin 4: Multiplicer eventuelle resterende faktorer i tælleren og/eller nævneren. Trin 1: Faktorer både tælleren og nævneren. Trin 2: Skriv som en brøk
