Indholdsfortegnelse:

Video: Hvordan løser man en absolutværdiligning algebraisk?

2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
LØSNING AF LIGNINGER, DER INDEHOLDER ABSOLUT(E) VÆRDI(ER)
- Trin 1: Isoler absolut værdi udtryk.
- Trin 2: Indstil mængden inde i absolut værdi notation lig med + og - mængden på den anden side af ligning .
- Trin 3: Løse for det ukendte i begge ligninger .
- Trin 4: Tjek dit svar analytisk eller grafisk.
Heraf, hvordan løser du absolutværdiligninger og uligheder?
Du begynder med at gøre det til to separate ligninger og så løse dem hver for sig. An absolut værdi ligning har ingen løsning, hvis absolut værdi udtryk er lig med et negativt tal, da an absolut værdi kan aldrig være negativ. Du kan skrive en absolut værdi ulighed som en forbindelse ulighed.
Derudover, hvad er den absolutte værdi for 4? Absolut værdi beskriver afstanden af et tal på tallinjen fra 0 uden at overveje, hvilken retning fra nul tallet ligger. Det absolut værdi af et tal er aldrig negativt. Det absolut værdi af 5 er 5.
Heraf, hvad er reglerne for absolut værdi?
Når vi tager absolut værdi af et tal, ender vi altid med et positivt tal (eller nul). Uanset om inputtet var positivt eller negativt (eller nul), er output altid positivt (eller nul). For eksempel | 3 | = 3, og | –3 | = 3 også.
Hvad er den absolutte værdi af 3?
For eksempel absolut værdi på 3 er 3 , og absolut værdi af - 3 er også 3 . Det absolut værdi af et tal kan opfattes som dets afstand fra nul.
Anbefalede:
Hvordan løser man en andengradsligning ved hjælp af nulfaktorloven?

Af dette kan vi udlede, at: Hvis produktet af to vilkårlige tal er nul, så er det ene eller begge tal nul. Det vil sige, hvis ab = 0, så er a = 0 eller b = 0 (hvilket inkluderer muligheden for, at a = b = 0). Dette kaldes nulfaktorloven; og vi bruger det ofte til at løse andengradsligninger
Hvordan ved man, om en absolutværdiligning ikke har nogen løsning?

Den absolutte værdi af et tal er dets afstand fra nul. Det tal vil altid være positivt, da du ikke kan være negativ to meter væk fra noget. Så enhver absolutværdiligning, der er lig med et negativt tal, er ingen løsning, uanset hvad det tal er
Hvordan finder man rødderne til en ligning algebraisk?

Rødderne af enhver andengradsligning er givet ved: x = [-b +/- sqrt(-b^2 - 4ac)]/2a. Skriv andengraden ned i form af ax^2 + bx + c = 0. Hvis ligningen er på formen y = ax^2 + bx +c, skal du blot erstatte y'et med 0. Dette gøres, fordi rødderne af ligning er de værdier, hvor y-aksen er lig med 0
Hvordan løser man et system af lineære ligninger algebraisk?

Brug eliminering til at løse den fælles løsning i de to ligninger: x + 3y = 4 og 2x + 5y = 5. x= –5, y= 3. Gang hvert led i den første ligning med –2 (du får –2x – 6y = –8) og læg derefter led i de to ligninger sammen. Løs nu –y = –3 for y, og du får y = 3
Hvordan finder man domænet for en algebraisk funktion?
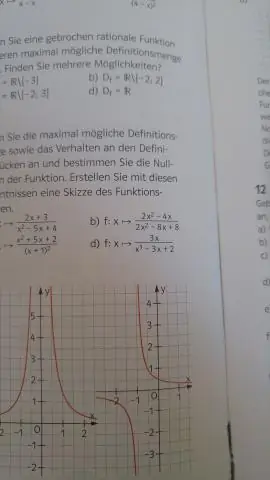
En funktions domæne er sættet af alle mulige input til funktionen. For eksempel er domænet for f(x)=x² alle reelle tal, og domænet for g(x)=1/x er alle reelle tal undtagen x=0
