Indholdsfortegnelse:

Video: Hvad er den trigonometriske formel?

2024 Forfatter: Miles Stephen | [email protected]. Sidst ændret: 2023-12-15 23:34
De seks trigonometrisk funktioner er sinus, cosinus, sekant, co-secant, tangent og co-tangens. Ved at bruge en retvinklet trekant som reference kan trigonometrisk funktioner eller identiteter udledes: sin θ = Modsatte Side/Hypotenuse. sek θ = Hypotenuse/tilstødende side.
På samme måde, hvad er formlerne for sin cos og tan?
Funktionerne af sin, cos og tan kan beregnes som følger:
- Sinus Funktion: sin(θ) = Modsat / Hypotenuse.
- Cosinus Funktion: cos(θ) = Adjacent / Hypotenuse.
- Tangentfunktion: tan(θ) = Modsat / Tilstødende.
Ligeledes, hvad er de 6 trigonometriske funktioner? For enhver retvinklet trekant er der seks trig-forhold: Sinus ( synd ), cosinus ( cos ), tangent (tan), cosecant (csc), sekant (sek), og cotangens (sengeseng).
Hvad er derfor de trigonometriske identiteter?
I matematik, trigonometriske identiteter er ligestilling, der involverer trigonometrisk funktioner og er sande for hver værdi af de forekommende variable, hvor begge sider af ligheden er defineret. Geometrisk er disse identiteter involverer visse funktioner af en eller flere vinkler.
Hvad er tan lig med?
Tangens af x er defineret til at være dens sinus divideret med dens cosinus: tan x = sin x cos x. Sekanten af x er 1 divideret med cosinus af x: sek x = 1 cos x, og cosecans af x er defineret til at være 1 divideret med sinus af x: csc x = 1 sin x.
Anbefalede:
Hvordan bruger du trigonometriske forhold til at finde sidelængder?

I enhver retvinklet trekant, for enhver vinkel: Vinklens sinus = længden af den modsatte side. længden af hypotenusen. Vinklens cosinus = længden af den tilstødende side. længden af hypotenusen. Tangens af vinklen = længden af den modsatte side. længden af den tilstødende side
Hvorfor studerer vi trigonometriske forhold?

Studiet af trigonometri involverer at lære, hvordan trigonometriske funktioner - såsom sinus eller cosinus for en vinkel, for eksempel - kan bruges til at beregne vinkler og dimensioner af en bestemt form. De bør også bruge disse funktioner i praktiske øvelser for at hjælpe eleverne med at udvikle deres færdigheder
Hvorfor kaldes trigonometriske funktioner cirkulære funktioner?

Trigonometriske funktioner kaldes nogle gange cirkulære funktioner. Dette skyldes, at de to grundlæggende trigonometriske funktioner - sinus og cosinus - er defineret som koordinaterne for et punkt P, der bevæger sig rundt på enhedscirklen med radius 1. Sinus og cosinus gentager deres udgange med regelmæssige intervaller
Hvad er empirisk formel og molekylær formel?
Molekylære formler fortæller dig, hvor mange atomer af hvert grundstof er i en forbindelse, og empiriske formler fortæller dig det enkleste eller mest reducerede forhold mellem grundstoffer i en forbindelse. Hvis en forbindelses molekylære formel ikke kan reduceres mere, så er den empiriske formel den samme som molekylformlen
Hvad er en strukturel formel Hvad er forskellen mellem en strukturel formel og en molekylær model?
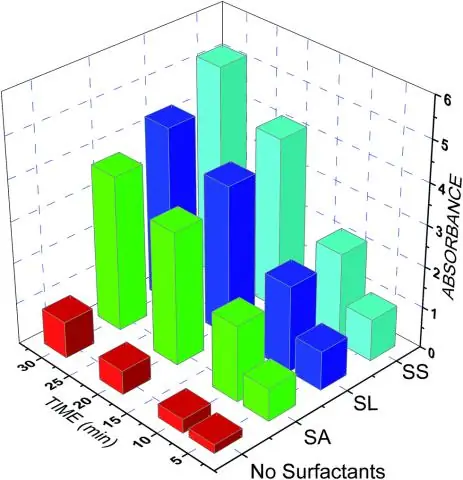
En molekylær formel bruger kemiske symboler og underskrifter til at angive det nøjagtige antal af forskellige atomer i et molekyle eller en forbindelse. En empirisk formel giver det enkleste hele talforhold mellem atomer i en forbindelse. En strukturel formel angiver bindingsarrangementet af atomerne i molekylet
